- ... espectral1
- O índice espectral
 para mapas da
temperatura de brilho se relaciona com o índice espectral
para mapas da
temperatura de brilho se relaciona com o índice espectral 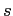 através da lei
de Rayleigh-Jeans, tal que se
através da lei
de Rayleigh-Jeans, tal que se 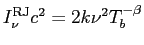 ,
então
,
então 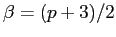 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Geminga2
- Geminga é uma
das fontes de raios-
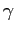 mais intensas do céu, mas sua verdadeira
natureza só foi revelada mais de 20 anos depois de sua descoberta a partir de
observações do satélite ROSAT de raios-X.
mais intensas do céu, mas sua verdadeira
natureza só foi revelada mais de 20 anos depois de sua descoberta a partir de
observações do satélite ROSAT de raios-X.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Sol3
- Medidas de paralaxe obtidas recentemente pelo telescópio
espacial Hubble para a contrapartida
no óptico do pulsar de Geminga estimam esta distância em
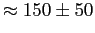 pc (Caraveo et al. 1996).
pc (Caraveo et al. 1996).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Reich4
- O mapa de Reich e Reich estende a cobertura em
declinação do mapa de Reich (
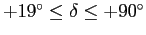 ) até
) até 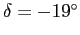 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... c\ ao.5
- Banday e
Wolfendale (1991a) mostraram que as flutuações do sinal do céu em
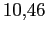 GHz resultavam menos ruidosos se a extrapolação em freqüência
fosse estimada com
GHz resultavam menos ruidosos se a extrapolação em freqüência
fosse estimada com ![$\beta_{[408,1420]}$](img213.png) , quando comparada com
, quando comparada com
![$\beta_{[408,820]}$](img214.png) ou
ou ![$\beta_{[820,1420]}$](img215.png) , utilizando o mapa em
820MHz de Berkhuijsen.
, utilizando o mapa em
820MHz de Berkhuijsen.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...G,6
- A relação clássica (Equação 9) não se
verifica na presença de uma população de elétrons relativísticos devido
ao alargamento do espectro de emissão de cada elétron. Nestas
circunstâncias uma dada freqüência recebe a contribuição de elétrons cujas
energias ocupam uma faixa considerável do espectro, tal que a
contribuição máxima se deve efetivamente a elétrons com
aproximadamente metade da energia prevista classicamente; ou seja,
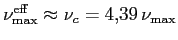 (Webber,
Simpson e Cane 1980).
(Webber,
Simpson e Cane 1980).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... mapas.7
- Estes mapas derivam dos observados mediante a
subtração das anisotropias de 1a e 2a ordens resultantes do
efeito Doppler. É natural esperar que o padrão quadrupolar da emissão
Galáctica se apresente correlacionado com as estruturas de origem
cosmológica nesse tipo de mapas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
DMR.8
- A cada mapa sintético se adiciona um de
ruído instrumental. O conceito do experimento DMR permite determinar
diretamente este nível, porque em cada freqüência operam dois canais,
cujos sinais somados produzem, em média, uma estimativa das variações
do sinal do céu, mas sua diferença resulta, em média, numa estimativa do
ruído instrumental.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...G)9
- Na análise dos dados de 4 anos do COBE, Kogut et al. (1996b) concluem que a normalização implica em
![$\beta_{[0,\!408;31,\!5]}>3,\!0$](img325.png) . Porém, como este valor implicaria num
valor inesperadamente baixo (
. Porém, como este valor implicaria num
valor inesperadamente baixo (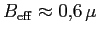 G) para o
campo magnético representativo da Galáxia, isto significa que a
calibração dos mapas em 408 e 1420 MHz está sujeita a incertezas
(Kogut 1996, comunicação pessoal). Recentemente,
Davies, Watson e Gutierrez (1996) apresentaram evidências conclusivas
de que as técnicas observacionais utilizadas nestes mapas também
introduzem efeitos instrumentais indesejáveis.
G) para o
campo magnético representativo da Galáxia, isto significa que a
calibração dos mapas em 408 e 1420 MHz está sujeita a incertezas
(Kogut 1996, comunicação pessoal). Recentemente,
Davies, Watson e Gutierrez (1996) apresentaram evidências conclusivas
de que as técnicas observacionais utilizadas nestes mapas também
introduzem efeitos instrumentais indesejáveis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.