BINGO

Receptor

O objetivo de um radiômetro é medir potência. Sua antena acopla a radiação eletromagnética com a entrada do radiômetro e como saída fornece uma potência média integrada em uma banda de frequência, ou seja, uma densidade de fluxo espectral. A densidade de fluxo espectral pode ser expressa por uma temperatura de brilho equivalente. Em um radiômetro ideal, a potência medida é diretamente proporcional à temperatura de brilho associada à fonte observada, como pode ser visto pela relação a seguir:

P = kBGT                                        (6.1)

onde k é a constante de Boltzmann, B a banda de frequência, G o ganho do receptor e T a temperatura.

A Figura 6.1 contém um esquema genérico de um radiômetro - doravante receptor - usado para medidas em rádio astronomia. O amplificador primário (LNA, caixa amarela) amplifica o sinal do céu e o envia para o segundo estágio, no qual um filtro (caixa verde) delimita a faixa de frequência que o telescópio observará. Esta etapa é muito importante pois existem bandas protegidas para radioastronomia, definidas pela União Internacional de Telecomunicações (UIT), dentro das quais outros sinais de rádio que contaminam as informações astronômicas são mantidos em níveis mínimos. No terceiro estágio, o sinal é misturado com um gerador de frequência intermediária (caixas vermelho e carmim) e é novamente amplificado, agora por um segundo amplificador (caixa azul), no quarto estágio. O objetivo de misturar a frequência de entrada com a intermediária é abaixá-la e facilitar o manuseio da saída. Em seguida, o sinal (até aqui, analógico) é somado pelo integrador (caixa azul) e passa por um conversor analógico-digital (caixa laranja claro) para ser transformado em digital (bytes em um computador) para ser armazenado por um computador (caixa cinza).

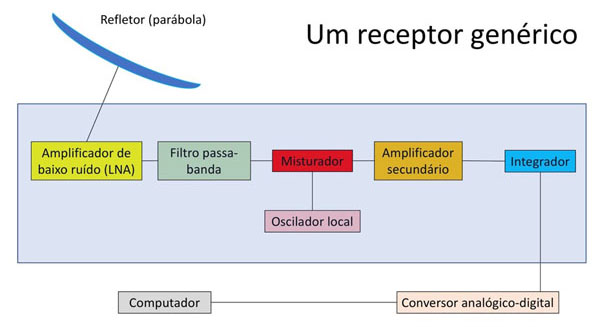
Figura 6.1: Cadeia de componentes de um receptor de rádio típico, começando pela parábola acima, à esquerda. Todas os componentes, do amplificador de baixo ruído ao integrador, antes que o sinal seja convertido para digital e chegue ao computador, são encapsulados em uma única caixa (no diagrama, a caixa azul semi-transparente).

Na figura 6.1, o gravador é representado por um computador, porém, antigamente, este registro era feito manualmente através de gráficos que eram "desenhados" mecanicamente e representavam as amplitudes dos sinais elétricos recebidos (Figura 6.2).

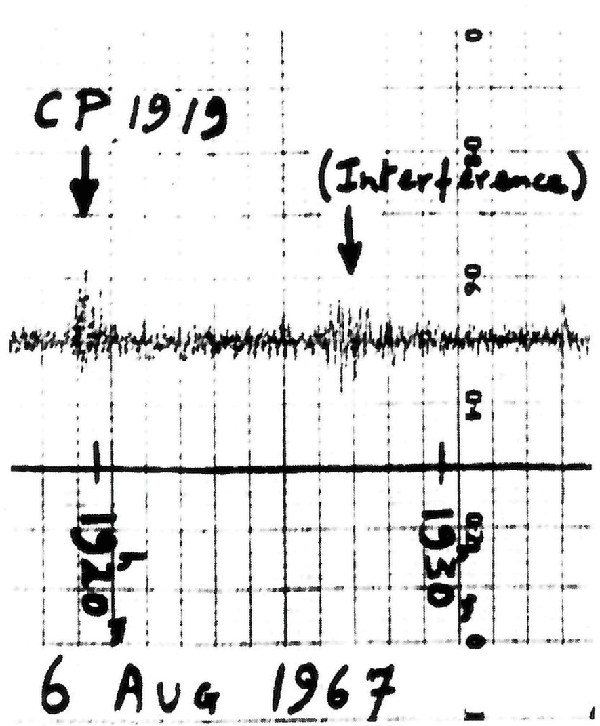
Figura 6.2: Sinal de medida de pulsars (Fonte: Hewitt, M. Cosmic Discoveries: the search, scope and heritage of Astronomy. Cambridge University Press, 2019).

Ganho, Figura de ruído e perda de retorno

O ganho G de um componente é a razão entre a potência de saída em relação à potência de entrada e é comumente medido em decibéis. O ganho é uma característica de componentes ativos, ou seja, que precisam ser alimentados por uma tensão. Um exemplo de componente ativo que apresenta ganho é o amplificador. Partindo da definição de decibel, pode-se encontrar o valor linear da amplificação de sinal através da relação:

G = 10G[dB]/10.                                        (6.2)

Como exemplo, um amplificador de ganho 20 dB aumenta em 100 vezes o nível de sinal de entrada. Já a Figura de ruído F está relacionada à temperatura de ruído de componentes ativos. É uma grandeza física também comumente medida em decibéis e pode ser transformada do mesmo modo que o ganho. A figura de ruído F relaciona-se com a temperatura de ruído do componente através da relação:

Tativo = Tamb(F - 1)                                        (6.3)

onde Tativo é a temperatura de ruído do componente ativo, Tamb é a temperatura ambiente que o componente está e F o valor linear da figura de ruído.

A perda de retorno P dos componentes representam a quantidade do sinal de entrada que é refletido pelo componente e também é usualmente medida em decibéis, transformando-se em um valor linear como as outras grandezas medidas em decibéis. A perda de retorno é uma característica de componentes passivos, ou seja, aqueles que não precisam de alimentação para funcionarem, como atenuadores e filtros seletores de banda. Ela está relacionada à temperatura de ruído dos componentes passivos através da relação:

Tpassivo = Tamb(P - 1)                                        (6.4)

onde Tpassivo é a temperatura de ruído de componentes passivos e P a perda de inserção na forma linear. A Figura 6.3 contém o esquema do receptor do BINGO, conforme mostrado na seção anterior.

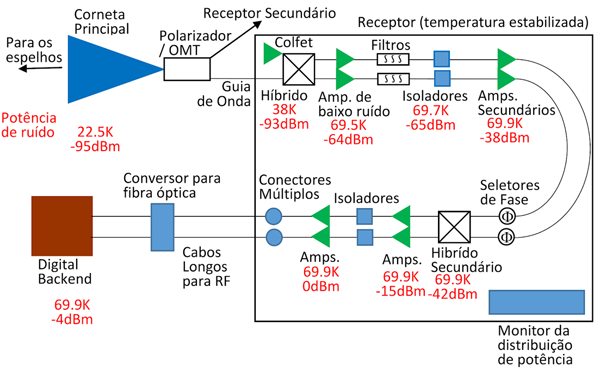
Figura 6.3: Diagrama em blocos - BINGO

Front End

O front end é responsável por adaptar os sinais vindos da corneta, que atua como "alimentador", para chegar até a cadeia de receptores, separando a polarização (circular) do sinal em esquerda (L) e direita (R). A decomposição do sinal é realizada para cada corneta através de dois guias de onda, um para cada polarização circular; cada sinal polarizado é combinado dentro de um magic tee e enviado à respectiva cadeia de amplificadores (parte superior da Figura 6.3, dentro do retângulo preto). Após o processamento, o sinal é "descombinado" ao passar pelo segundo "hybrid", amplificado novamente e então enviado ao Digital Back End (DBE), responsável pelo separação do sinal integrado (lembre-se que a banda do BINGO vai de 980 a 1260 MHz) em diferentes bandas de frequência, através de uma Transformada de Fourier (FFT) realizada via hardware.

Back End

Desde meados dos anos 60, o Processamento Digital de Sinais (Digital Signal Processing – DSP) via hardware vem sendo muito importante para os radiotelescópios. Atualmente o emprego de computadores com alta capacidade de processamento, Arranjos de Portas Programáveis em Campo (Field-Programmable Gate Arrays – FPGAs), Circuitos Integrados de Aplicação Específica (Application Specific Integrated Circuits – ASICs), dentre outras tecnologias, é praticamente obrigatório em todos os novos radiotelescópios do mundo.

A Colaboração para Processamento de Sinais de Astronomia e Pesquisa Eletrônica (Collaboration for Astronomy Signal Processing and Electronics Research – CASPER https://casper.berkeley.edu) é um grupo formado por membros dos radiotelescópios mais importantes do mundo e que visa a desenvolver receptores digitais de última geração.

Um destes é o hardware de computação de arquitetura aberta reconfigurável (Reconfigurable Open Architecture Computing Hardware – ROACH), que se trata de uma placa FPGA única, dispensando conexões internas entre as placas e adotando interfaces de alta velocidade para todas as comunicações necessárias. O ROACH 2 foi desenvolvido como evolução do ROACH 1 usando uma nova série de FPGAs. Mantendo todos os aspectos que tornaram a primeira versão do ROACH muito eficiente e suas compatibilidades, acrescenta desempenho em capacidade de processamento, nas taxas de transferências de entrada e saída e na largura de banda da memória.

Sucessor do ROACH e do ROACH 2, a placa de aplicação reconfigurável da matriz de quilômetros quadrados (Square Kilometre Array Reconfigurable Application Board – SKARAB), prevê mais interfaces suportando 16 transceptores seriais de alta velocidade (Figura 6.4).

O design do SKARAB previu um módulo para ser montado em rack de 1U, contendo uma grande placa de circuito impresso, um FPGA Xilinx Virtex 7 FPGA com capacidade de processamento de 693120 células lógicas, 80 canais SERDES (Serializer/Deserializer) e 1470 blocos de RAM de 32kb (Figura 6.5).

Ruídos em Sinais de Rádio

Tratam-se de sinais indesejados que estão justapostos ao sinal desejado (útil) e podem ser vários tipos de perturbações que tendem a atrapalhar as observações, provenientes de várias causas (eletrônicos, interferências de sinais externos). Há relatos de equipamentos domésticos de micro-ondas terem causado grandes confusões por um tempo considerável nas observações.

Como forma de tentar minimizar os efeitos destes ruídos nas medidas analíticas, são empregados filtros digitais.

Como os sinais desejados apresentam baixa intensidade é necessário que estes sejam amplificados. Neste estágio são empregados amplificadores, ou seja, dispositivos ativos que interferem eletricamente nos sensores.

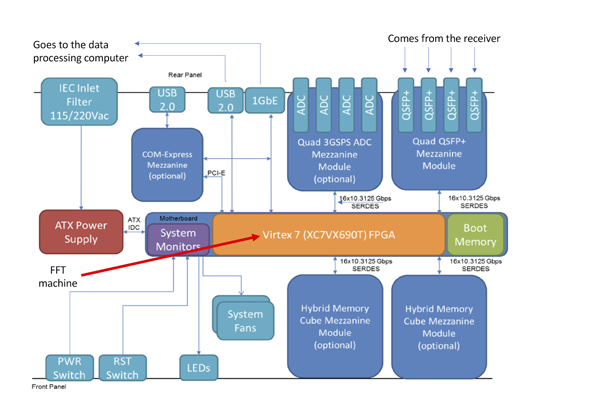
Figura 6.4: Diagrama de Blocos do SKARAB. (Fonte: https://casper.ssl.berkeley.edu/wiki/SKARAB).

A fim de se minimizar os efeitos destas interferências nas medidas é necessária a filtragem antes da propagação do sinal. Esta operação geralmente é mais eficiente no domínio da frequência no qual um espectro com as intensidades das diversas frequências presentes no sinal pode ser obtido pela aplicação da Transformada de Fourier.

Essa transformada tem como objetivo tomar um sinal com representação no domínio do tempo e representá-lo no domínio da frequência, o que é feito separando as frequências que compõem o sinal no domínio do tempo, medindo a intensidade de cada uma destas frequências e compondo um espectro formado por pulsos nas frequências (Figura 6.6).

Quanto menos significativa for uma determinada parcela do sinal, menor será o pulso obtido na transformada. Esta característica é muito útil para a filtragem do sinal uma vez que facilita a seleção das componentes de maior interesse, descartando-se o que não for de interesse para a análise.

Figura 6.5: SKARAB. (Fonte: http://www.tauceti.caltech.edu/casper-workshop-2017/slides/12_moschella.pdf).

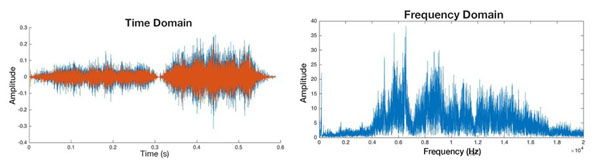
Figura 6.6: Exemplo de uma forma de onda no domínio do tempo (esquerda) e no domínio da frequência (direita). (Fonte da figura: Moore, Dylan & Tennent, Hamish & Martelaro, Nikolas & Ju, Wendy. (2017). Making Noise Intentional: A Study of Servo Sound Perception).

O algoritmo da FFT decompõe a matriz de um sinal qualquer em amplas frequências, complexas e específicas o bastante para seguirem a um padrão de leitura e codificação. As frequências com latência muito baixa podem ser desconsideradas, permitindo, também, uma boa compressão de dados. Este método se destaca em processamento digital de sinais pelo fato de que as operações domínio da frequência são igualmente viáveis computacionalmente como o trabalho no domínio temporal ou espacial.

Podem ser destacadas as seguintes aplicações da FFT:

• Multiplicação rápida de números inteiros e polinomiais
• Algoritmos de filtragem (Figura 6.7).
• Algoritmos rápidos para transformações discretas de cosseno ou seno (por exemplo as codificações JPEG, MP3 e MPEG)
• Resolução de Equações Diferenciais
• Computação de distribuições isotópicas.

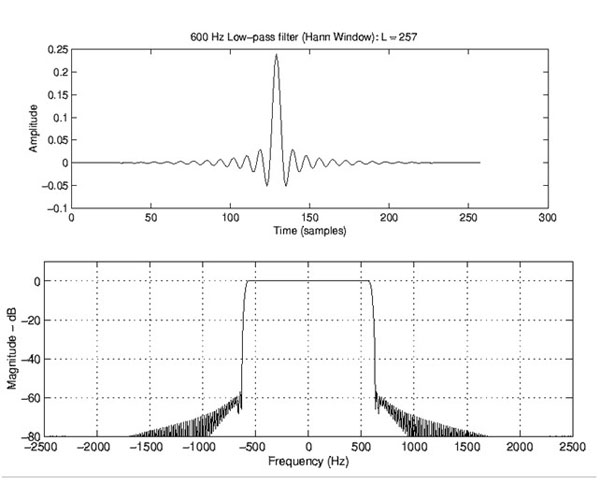
Figura 6.7: Exemplo de Filtro Passa Baixas (Low-Pass Filter – LPF). (Fonte: https://ccrma.stanford.edu/~jos/sasp//Example_1_Low_Pass_Filtering.html).

Referências

1. "Inside the FFT black box: serial and parallel fast Fourier transform algorithms" (1950-, Chu, Eleanor Chin-Hwa, 2000)
2. "The FFT: an algorithm the whole family can use" (Rockmore, D.N. (2000), Computing in Science & Engineering. 2 (1): 60-64).