Cosmologia

O efeito Sunyaev-Zel'dovich

1 – Introdução

O efeito Sunyaev-Zel’dovich (doravante SZ) foi previsto por R. Sunyaev e Y. B. Zel’dovich no inicio da década de 70 ([7]) e vem se tornando uma ferramenta bastante interessante para mapear estruturas em grande escala no Universo, em particular na escala de aglomerados de galáxias (z ~ 0, 01 até z > 2). Artigos de revisão sobre a física do efeito SZ vêm sendo escritos desde 1980 e sua leitura permite acompanhar a evolução das observações desde a década de 80 e as perspectivas de seu uso, cada vez mais amplo, em cosmologia ([9], [12], [11], [6], [10]).

O efeito SZ é causado pelo espalhamento Compton inverso de elétrons de altas temperaturas em aglomerados sobre os fótons da RCFM, deslocando-os para frequências mais altas. A energia típica dos elétrons nos aglomerados é dada por:

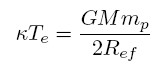
em que k é a constante de Boltzmann, Te é a temperatura dos elétrons, G é a constante de gravitação, M é a massa do aglomerado, mp é a massa do próton e Ref é o raio efetivo do aglomerado. A taxa de ganho de energia dos fótons é dada pela relação

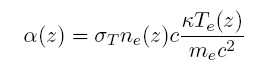
em que α(z) é a taxa de ganho de energia dos fótons como função do "redshift", σT é a seção de choque para o espalhamento Thomson, k é a constante de Boltzmann, T_e é a temperatura dos elétrons, n_e é a densidade eletrônica, m_e é a massa do elétron e c é a velocidade da luz. O ganho total de energia obtido pelos fótons é conhecido como o parâmetro de comptonização y e é dado pela relação

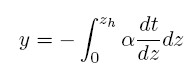
Esse processo de transferência de energia faz com que o espectro de corpo negro seja trasladado para frequências mais altas. A frequência de inversão do regime de Rayleigh-Jeans para o regime de Wien ocorre quando T´ = T0. No limite de pequenos y, νc ≈ 3,83 KT/h ([1]).

Ele oferece algumas vantagens em relação aos métodos baseados em imageamento óptico ou em raios-X, entre elas a boa eficiência de detecção em grandes "redshifts", uma seleção baseada na energia térmica do meio intra-aglomerado, o fato de ser uma quantidade robusta comparativamente a qualquer estrutura térmica do gás intra-aglomerado e um limite de detecção de massa em função do "redshift" praticamente constante (ver, p.ex., [2], [3], [4]). A determinação de parâmetros cosmológicos usando medidas do efeito SZ é potencializada combinando-as com outras técnicas de estudo de aglomerados, tais como emissão de raios-X do meio intergaláctico, o efeito (forte e fraco) de lentes gravitacionais causado pelo potencial gravitacional do aglomerado e medidas ópticas da dispersão de velocidades das galáxias no aglomerado.

A essência das medidas do efeito SZ envolve a estimativa da densidade numérica de elétrons em função da distância ao centro do aglomerado e a integração da equação 1 para encontrar o valor de y. Para aglomerados ricos, y ~ 10^-4 ao longo da linha de visada passando pelo centro do aglomerado.

A amplitude e o tamanho angular do efeito permitem extrair informações sobre a distribuição espacial, densidade e temperatura do plasma intergaláctico nos aglomerados. A combinação de medidas do efeito SZ com observações em raios-X permitem a determinação direta da distância ao aglomerado.

Combinando as medidas de ΔT/T (independentes da distância) com medidas de raios-X (∝ 1/d²), estimamos o valor de H₀ utilizando a Lei de Hubble.

2 - Os efeitos SZ térmico e cinemático

O efeito conhecido como SZ térmico é caracterizado por uma pequena distorção espectral, da ordem de 1mK e independe do redshift. O pico do espectro de corpo negro que sofre a distorção SZ é uma função da temperatura do gás de elétrons (Te). No limite relativístico para os elétrons (hn << m_ec²), a frequência de pico pode ser calculada a partir da relação x = 3, 83(1 + kT_e/m_ec²) em que x = hν/kT_RCF e encontra-se próxima a 220 GHz. Reescrevendo a eq. 3, obtemos:

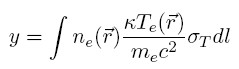
em que a integração é feita ao longo da linha de visada, n_e e T_e, numa análise mais refinada, dependem da distância angular em relação ao centro do aglomerado. O significado dos parâmetros é o mesmo das equações anteriores. Devido à forma como este efeito é gerado, o fluxo integrado é proporcional à massa ponderada pela temperatura do aglomerado. Isso fornece um limiar de massa praticamente independente do "redshift" em que o aglomerado se encontra.

O efeito SZ cinemático é causado pelo movimento peculiar de aglomerados e sua amplitude é ~ 10% da amplitude do efeito SZ térmico. O efeito Doppler da velocidade do aglomerado é somado aos fótons espalhados, causando um efeito tipicamente não-relativístico, dado por

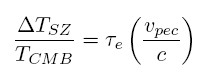
A velocidade transversal de um aglomerado produz, ainda, um efeito SZ de segunda ordem que polariza os fótons espalhados da RCFM. Existem dois efeitos separados discutidos por Sunyaev e Zel’dovich: um proporcional a (v/c)²y (da ordem de 1% do efeito térmico) e outro proporcional a (v/c) y² da ordem de 0,2% do efeito térmico), em que y, obtido da equação 3, determina a amplitude do sinal SZ.

3 - A polarização da RCFM e o efeito SZ

A polarização dos fótons da RCFM devido ao espalhamento pelos elétrons quentes do meio intra-aglomerado produz radiação polarizada com amplitude proporcional a potências de (vpec/c) e τ_e, cujas amplitude e padrão de polarização devem variar claramente do centro para as bordas do aglomerado.

O padrão deve ser razoavelmente bem comportado (concêntrico ou radial) no caso de uma distribuição esférica de gás, tornando-se mais e mais complexo à medida que a distribuição deixa de ser esfericamente simétrica. Sazonov e Sunyaev ([14]) calculam diversos padrões de polarização e mostram que o pico de polarização deste sinal será da ordem 0, 025(kTe/ m_ec²)τ²_e × I_RCF. Um aglomerado massivo cujo gás possui τ_e = 0, 01 gerará um efeito de 0,1 μK no sentido da borda do aglomerado. A polarização do efeito SZ é inteiramente produzida pela componente de quadrupolo do campo de radiação local.Nesse caso, a componente de quadrupolo nas bordas do aglomerado é causada pelo anisotropia no campo de radiação na direção do centro do aglomerado devido ao efeito SZ. Existe ainda uma contribuição ao efeito SZ cinemático proporcional à velocidade peculiar transversal à linha de visada. Sazonov e Sunyaev ([14]) encontraram, para τe = 0, 01 e vpec ~ 500 km.s^-1, níveis de polarização da ordem de 10nK, muito abaixo do nível de sensibilidade dos instrumentos atuais.

4 - Status das observações

Desde os artigos iniciais de Sunyaev e Zel’dovich sobre o tema deste trabalho ([7], [8]), os resultados obtidos saíram de diversas estimativas de limites superiores e algumas poucas detecções (até aproximadamente 1993) para resultados com boa relação sinal-ruído e imagens da região observada, de 1995 a 2005. Neste momento, uma série de experimentos estão sendo realizados para estudar o impacto do efeito SZ na busca de aglomerados de galáxias e o levantamento SZ do satélite Planck é ansiosamente esperado.

A grande evolução de qualidade nas medidas do efeito SZ deveu-se principalmente a um melhor entendimento dos erros sistemáticos. O conhecimento da função de seleção de um determinado levantamento é um pré-requisito essencial para qualquer aplicação estatística no levantamento, caso contrário não se terá a mínima idéia de quão representativa da população original é a amostra estudada.

5 - Implicações de observações do efeito SZ para astrofísica e cosmologia

Levantamentos do efeito SZ fornecerão excelentes catálogos para a utilização em estudos cosmológicos, permitindo a exploração direta do Universo em grandes "redshifts", bem como a oportunidade de determinar alguns parâmetros cosmológicos, tais como a medida de distância a aglomerados e da constante de Hubble, a razão Ω_b/Ω_M e velocidades peculiares dos aglomerados. A determinação ótima dependerá da combinação adequada das medidas do efeito SZ e de outras medidas, tais como efeitos de lentes gravitacionais, medidas no óptico e em raios-X. Particularmente estamos interessados na possibilidade de verificar como a polarização da RCFM produzida nos aglomerados reflete o quadrupolo na temperatura da RCFM. Como é possível observar aglomerados em diversas direções do céu e "redshifts", é possível utilizar a polarização observada para inferir algum efeito evolutivo no quadrupolo, bem como tentar diminuir a variância cósmica ao observar o quadrupolo em uma região muito afastada de nós ([15], [14]).

Os principais desafios no estudo do efeito SZ estão ligados ao conhecimento da física de aglomerados. Particularmente, efeitos causados pela dinâmica do gás, tais como a dependência do efeito SZ com a densidade numérica de elétrons, os efeitos de normalização e evolução com o "redshift" da relação entre o efeito SZ e a massa do aglomerado e o mapeamento entre o campo de densidades primordial e a densidade numérica de aglomerados de uma dada massa como função do "redshift" são alguns dos problemas que ainda devem ser atacados nos próximos anos, para que seja possível explorar em detalhes os próximos catálogos de fontes SZ, particularmente a que será gerada pelo satélite Planck ([10]). Para isso, é necessário conhecer os detalhes da função de massa de aglomerados e a massa limite de aglomerados como função do redshift com precisão melhor que, respectivamente, 5% e 10% ([16]).

Referências

1. Partridge, B. “3 K: The cosmic microwave background radiation”, Cambridge University Press, págs. 170-173, 1995.
2. Holder, G. P. et al. “Expectations for an Interferometric Sunyaev-Zeldovich Effect Survey for Galaxy Clusters”. 2000, ApJ, 544, 629
3. Bartlett, J. G. arXiv: astro-ph/0001267
4. Bartlett, J. G. Review in “Tracing cosmic evolution with galaxy clusters”, Sesto Pueria, 3-6 July 2001, ASP Conf. Series, in press [arXiv:astro-ph/0111211]
5. Melin, J.-B; Bartlett, J. G.; Delabrouille, J. “The selection function of SZ cluster surveys”. Astronomy&Astrophysics, 429, 417, 2005
6. Birkinshaw, M. “The Sunyaev-Zel’dovich effect”. Physics Reports, 310, 97-195, 1999
7. Sunyaev, R.; Zel’dovich, Ya. B. “The Spectrum of Primordial Radiation, its Distortions and their Significance”. Comments on Astrophysics and Space Science, 2, 66, 1970
8. Sunyaev, R.; Zel’dovich, Ya. B. “The observation of relic radiation as a test of the nature of X-ray radiation from the clusters of galaxies”. Comments on Astrophysics and Space Science, 4, 173, 1972
9. Sunyaev, R.; Zel’dovich, Ya. B. “Microwave background radiation as a probe of the contemporary structure and history of the Universe”. Annual Review of Astronomy and Astrophysics, 18, 537, 1980
10. Carlstrom, J.; Holder, G.; Reese, E. “Cosmology with the Sunyaev- Zel’dovich effect”. Annual Review of Astronomy and Astrophysics, 40, 643-680, 2002.
11. Rephaeli, Y. “Comptonization of the cosmic microwave background: the Sunyaev-Zel’dovich effect”. Annual Review of Astronomy and Astrophysics, 33, 541-579, 1995
12. Bernestein, J.; Dodelson, S. “Aspects of the Sunyaev-Zel’dovich mechanism”. Physical Review D, 41, 354-373, 1990.
13. Kosowsky, A. “The future of Microwave Background Physics”. [arXiv:astro-ph/0301131], 2003
14. Sazonov, S.; Sunyaev, R. “Microwave polarization in the direction of galaxy clusters induced by the CMB quadrupole anisotropy”. Montly Notices of the Royal Astronomical Society, 310, 765-772, 1999
15. Abramo, L.R.W. Comunicação pessoal
16. Holder, G. P.; Haiman, Z.; Mohr, J. J. “Constraints on WM, WL and s8 from Galaxy Cluster Redshift Distributions”. The Astrophysical Journal, 560, L111-L114, 2001.