Cosmologia
Testes clássicos
Os cenários previstos pelo MCP para um Universo homogêneo e isotrópico em expansão dependem essencialmente da densidade de energia e matéria e da taxa de expansão do Universo. A curvatura do espaço-tempo, criada pela presença de matéria no Universo, desempenha um importante papel na interpretação de informações sobre luminosidade, distância, idade, tamanho angular e densidade numérica de objetos extragalácticos. Testes cosmológicos clássicos examinam esses observáveis na tentativa de refinar medidas de alguns parâmetros que descrevem o Universo, como a constante de Hubble H₀ e o parâmetro de desaceleração q₀.
Mattig, em 1958, e Terrell, em 1977, mostraram que, para um universo homogêneo e isotrópico com constante cosmológica ∧ = Ο, a relação magnitude-redshift é dada por
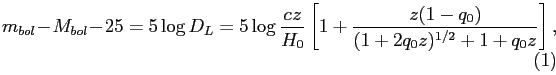
em que mbol é a magnitude bolométrica aparente, Mbol é a magnitude bolométrica absoluta, DL é a distância de luminosidade em Mpc (megaparsecs), c é a velocidade da luz, z é o deslocamento para o vermelho (redshift), H₀ é a constante de Hubble e q₀ é o parâmetro de desaceleração. Teoricamente, a relação de Mattig pode ser usada para relacionar os observáveis mbol e z com os parâmetros H₀ e q₀. Entretanto, limitações de sensibilidade dos detectores, processos físicos que ocorrem nas estrelas e no meio interestelar e variações na magnitude aparente de objetos distantes exigem cálculos complicados para corrigir as quantidades envolvidas na Equação (1). Na prática, essas correções introduzem erros que impedem que alguma conclusão definitiva sobre diferentes cenários cosmológicos possa ser inferida a partir da relação de Mattig. Porém, essa relação continua sendo importante, pois todos os testes cosmológicos que envolvem a grandeza DL podem ser diretamente relacionados ao redshift z e aos parâmetros H₀ e q₀.
Outro teste cosmológico clássico é a contagem de galáxias em função da magnitude aparente. Se as galáxias estão uniformemente distribuídas no céu e possuem a mesma luminosidade absoluta L, então o número de galáxias com fluxo aparente superior a f será dado por
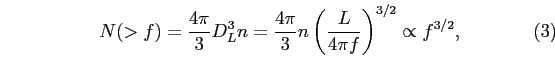
em que n é a densidade de galáxias. Portanto, o número de galáxias com magnitude aparente menor que m será
Esse teste pode indicar se a distribuição de galáxias em grande escala é de fato uniforme. O Telescópio Hubble vem sendo usado para estender as contagens de galáxias até m ≈ 30 e z ~ 5. Entretanto, esses números ainda não fornecem uma prova definitiva da geometria do Universo. Fontes que emitem em rádio permitem realizar contagens em redshifts maiores do que fontes que emitem no óptico. Em um universo euclidiano estático, a contagem do número de fontes de rádio, por unidade de ângulo sólido, com densidade de fluxo maior que S deve obedecer à relação
Eventuais desvios de uma inclinação −1,5 (numa escala logarítmica) permitiriam selecionar um (ou alguns) cenário(s) cosmológico(s) que se ajusta(m) bem às observações. Porém, um excesso significativo de radiofontes tem sido encontrado em comparação ao que se esperaria no MCP. O aumento observado em N quando S decresce não pode ser explicado por efeitos de curvatura no espaço-tempo. A contagem de radiofontes fornece muito mais informação sobre a evolução das galáxias do que sobre a geometria do Universo, porque há enormes mudanças nas propriedades das galáxias para diferentes redshifts.
A variação no diâmetro angular aparente de fontes cósmicas, θ, em função do redshift, z, também pode ser usada como teste cosmológico. Em um universo isotrópico e homogêneo em expansão, uma fonte cósmica com diâmetro linear intrínseco l deve ter um diâmetro ângular aparente dado por
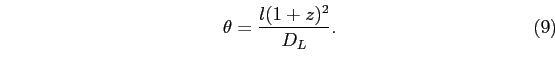
Para um universo homogêneo e isotrópico em expansão com q₀ > 0, o tamanho angular aparente dessa fonte diminui com o aumento do redshift até atingir um mínimo absoluto em um dado Zmin finito. A partir de então, θ aumenta com z. Por exemplo, se q₀ = 0,5 então θ é mínimo para Zmin = 1,25. Esse teste já foi aplicado a radiofontes que possuem lóbulos duplos até z ≈ 2 sem que nenhum Zmin tenha sido detectado. Efeitos de seleção, porém, comprometem eventuais conclusões obtidas a partir deste teste. Por exemplo, objetos intrinsicamente mais luminosos são preferencialmente observados em grandes distâncias. Além disso, o teste não leva em conta de que forma o tamanho das galáxias varia com o tempo.
Os resultados obtidos com os testes cosmológicos clássicos discutidos acima são consistentes com um universo homogêneo e isotrópico em expansão, mas a dispersão dos dados torna impossível usá-los para escolher o melhor dentre os diferentes cenários cosmológicos. Os experimentos atuais não têm a precisão neces-sária para inferir conclusões definitivas, mas sugerem que objetos extragalácticos evoluem no tempo. Felizmente, existem outros testes (não-clássicos) que também permitem extrair parâmetros cosmológicos a partir de observáveis físicos. Por exemplo, estimativas obtidas da Radiaçao Cósmica de Fundo em Microondas indicam que o Universo tem 13,7 x 109 anos, H0 ≃ 71 km s -1 Mpc-1, Ω ≃ 1,0, Ωm ≃ 0,3, Ω ≃ 0,4.
Carlos Alexandre Wuensche - Criado em 2005-06-02







